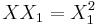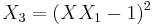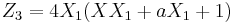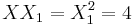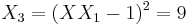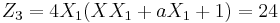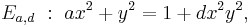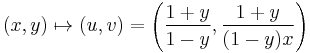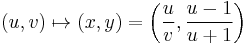Montgomery curve
In mathematics the Montgomery curve is a form of elliptic curve, different from the usual representation (Weierstrass form). It has been introduced by Peter L.Montgomery in,[1] and it has been used since 1987 for certain computations, and in particular in different cryptography applications.
Contents |
Definition
A Montgomery curve over a field  is defined by the equation:
is defined by the equation:
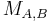 :
: 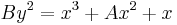
for certain 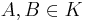 and with
and with 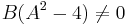 .
.
Generally this curve is considered over a finite field  (for example over a finite field of q elements,
(for example over a finite field of q elements, 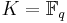 ) with characteristic different from 2 and with
) with characteristic different from 2 and with 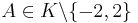 ,
, 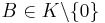 ; but they are also considered over the rationals with the same restrictions for A and B.
; but they are also considered over the rationals with the same restrictions for A and B.
Montgomery arithmetic
It is possible to do some "operations" between the points of an elliptic curve: "adding" two points 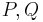 consists on finding a third one
consists on finding a third one  such that
such that 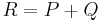 ; "doubling" a point consists on computing
; "doubling" a point consists on computing ![[2]P=P%2BP](/2012-wikipedia_en_all_nopic_01_2012/I/347606ce1c02921cb4d69ae998bc70ec.png) (For more information about operations see The group law) and below.
(For more information about operations see The group law) and below.
A point 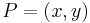 on the elliptic curve in the Montgomery form
on the elliptic curve in the Montgomery form 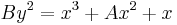 can be represented in Montgomery coordinates
can be represented in Montgomery coordinates 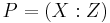 , where
, where 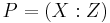 are projective coordinates and
are projective coordinates and 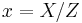 for
for 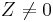 .
.
Notice that this kind of representation for a point loses information: indeed, in this case, there is no distinction between the affine points 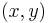 and
and 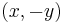 because they are both given by the point
because they are both given by the point 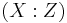 . However, with this representation it is possible to obtain multiples of points, that is, given
. However, with this representation it is possible to obtain multiples of points, that is, given 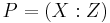 , to compute
, to compute ![[n]P=(X_n:Z_n)](/2012-wikipedia_en_all_nopic_01_2012/I/ae58cb54540fbf8028431e86e3a98170.png) .
.
Now, considering the two points ![P_n=[n]P=(X_n:Z_n)](/2012-wikipedia_en_all_nopic_01_2012/I/303e98fecdf8b98a2dfa6a52a9e0b05c.png) and
and ![P_m=[m]P(X_m:Z_m)](/2012-wikipedia_en_all_nopic_01_2012/I/e60d219fc0faf3a577be1143c93b90eb.png) : their sum is given by the point
: their sum is given by the point 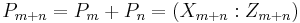 whose coordinates are:
whose coordinates are:
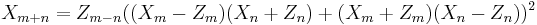
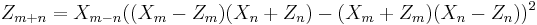
If 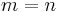 , then the operation becomes a "doubling"; the coordinates of
, then the operation becomes a "doubling"; the coordinates of ![[2]P_n=P_n%2BP_n=P_{2n}=(X_{2n}:Z_{2n})](/2012-wikipedia_en_all_nopic_01_2012/I/9c64c84b7c71c16853e3f1be67098684.png) are given by the following equations:
are given by the following equations:
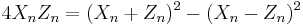
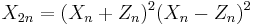
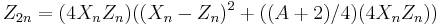
The first operation considered above (addition) has a time-cost of 3M+2S, where M denotes the multiplication between two general elements of the field on which the elliptic curve is defined, while S denotes squaring of a general element of the field.
The second operation (doubling) has a time-cost of 2M+2S+1D, where D denotes the multiplication of a general element by a constant; notice that the constant is 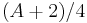 , so
, so  can be chosen in order to have a small D.
can be chosen in order to have a small D.
Algorithm and example
The following algorithm represents a doubling of a point 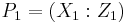 on an elliptic curve in the Montgomery form.
on an elliptic curve in the Montgomery form.
It is assumed that 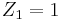 . The cost of this implementation is 1M + 2S + 1*A + 3add + 1*4. Here M denotes the multiplications required, S indicates the squarings, and a refers to the multiplication by A.
. The cost of this implementation is 1M + 2S + 1*A + 3add + 1*4. Here M denotes the multiplications required, S indicates the squarings, and a refers to the multiplication by A.
Example
Let 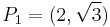 be a point on the curve
be a point on the curve 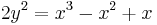 . In coordinates
. In coordinates 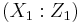 , with
, with 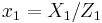 ,
, 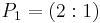 .
.
Then:
The result is the point 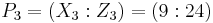 , such that
, such that 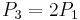 .
.
Addition
Given two points 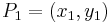 ,
, 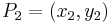 on the Montgomery curve
on the Montgomery curve 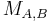 in affine coordinates, the point
in affine coordinates, the point 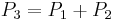 represents, geometrically the third point of intersection between
represents, geometrically the third point of intersection between 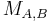 and the line passing through
and the line passing through 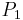 and
and 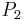 . It is possible to find the coordinates
. It is possible to find the coordinates 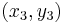 of
of 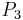 , in the following way:
, in the following way:
1) consider a generic line y=lx+m in the affine plane and let it pass through 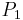 and
and 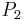 (impose the condition), in this way, one obtains
(impose the condition), in this way, one obtains 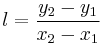 and
and 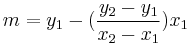 ;
;
2) intersect the line with the curve 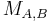 , substituting the y variable in the curve equation with y=lx+m; the following equation of third degree is obtained:
, substituting the y variable in the curve equation with y=lx+m; the following equation of third degree is obtained:
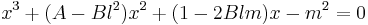 .
.
As it has been observed before, this equation has three solutions that correspond to the x coordinates of 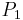 ,
, 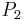 and
and 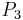 . In particular this equation can be re-written as:
. In particular this equation can be re-written as:
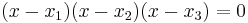
3) Comparing the coefficients of the two identical equations given above, in particular the coefficients of the terms of second degree, one gets:
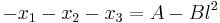 .
.
So, 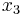 can be written in terms of
can be written in terms of 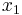 ,
, 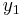 ,
, 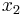 ,
, 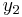 , as:
, as:
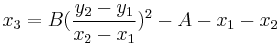 .
.
4) To find the y coordinate of the point 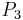 it is sufficient to substitute the value
it is sufficient to substitute the value 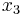 in the line y=lx+m. Notice that this will not give the point
in the line y=lx+m. Notice that this will not give the point 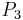 directly. Indeed, with this method one find the coordinates of the point R such that
directly. Indeed, with this method one find the coordinates of the point R such that 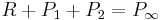 , but if one needs the resulting point of the sum between
, but if one needs the resulting point of the sum between 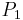 and
and 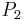 , then it is necessary to observe that:
, then it is necessary to observe that: 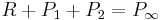 if and only if
if and only if 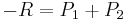 . So, given the point R, it is necessary to find -R, but this can be done easily by changing the sign to the y coordinate of R. In other words, it will be necessary to change the sign of the y coordinate obtained by substituting the value
. So, given the point R, it is necessary to find -R, but this can be done easily by changing the sign to the y coordinate of R. In other words, it will be necessary to change the sign of the y coordinate obtained by substituting the value 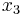 in the equation of the line.
in the equation of the line.
Resuming, the coordinates of the point 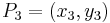 ,
, 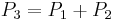 are:
are:
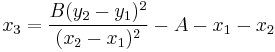
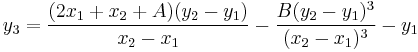
Doubling
Given a point 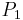 on the Montgomery curve
on the Montgomery curve 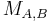 , the point
, the point ![[2]P_1](/2012-wikipedia_en_all_nopic_01_2012/I/1daaf3fc1b93cf1b3ae06c9fee7d4aa0.png) represents geometrically the third point of intersection between the curve and the line tangent to
represents geometrically the third point of intersection between the curve and the line tangent to  ; so, to find the coordinates of the point
; so, to find the coordinates of the point 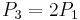 it is sufficient to follow the same method given in the addition formula; however, in this case, the line y=lx+m has to be tangent to the curve at
it is sufficient to follow the same method given in the addition formula; however, in this case, the line y=lx+m has to be tangent to the curve at 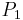 , so, if
, so, if 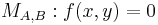 with
with
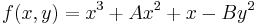 ,
,
then the value of l, which represents the slope of the line, is given by:
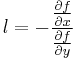
by the implicit function theorem.
So 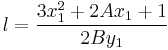 and the coordinates of the point
and the coordinates of the point 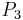 ,
, 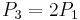 are:
are:
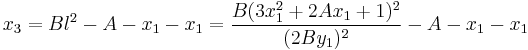
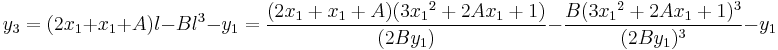 .
.
Equivalence with twisted Edwards curves
Let  be a field with characteristic different from 2.
be a field with characteristic different from 2.
Let 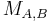 be an elliptic curve in the Montgomery form:
be an elliptic curve in the Montgomery form:
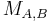 :
: 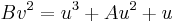
with 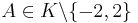 ,
, 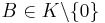
and let 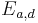 be an elliptic curve in the twisted Edwards form:
be an elliptic curve in the twisted Edwards form:
with 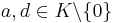 ,
, 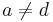 .
.
The following theorem proved in,[2] shows the birational equivalence between Montgomery curves and an twisted Edwards curves:
Theorem (i) Every twisted Edwards curve is birationally equivalent to a Montgomery curve over  . In particular, the twisted Edwards curve
. In particular, the twisted Edwards curve 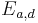 is birationally equivalent to the Montgomery curve
is birationally equivalent to the Montgomery curve 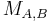 where
where 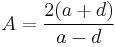 , and
, and 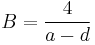 .
.
The map:
is a birational equivalence from 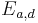 to
to 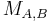 , with inverse:
, with inverse:
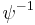 :
: 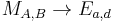
Notice that this equivalence between the two curves is not valid everywhere: indeed the map  is not defined at the points
is not defined at the points 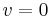 or
or 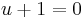 of the
of the 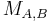 .
.
Equivalence with Weierstrass curves
Any elliptic curve can be written in Weierstrass form.
So, the elliptic curve in the Montogmery form
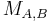 :
: 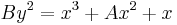 ,
,
can be transformed in the following way: divide each term of the equation for 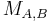 by
by 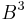 , and substitute the variables x and y, with
, and substitute the variables x and y, with 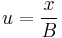 and
and 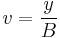 respectively, to get the equation
respectively, to get the equation
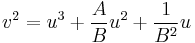 .
.
To obtain a short Weierstrass form from here, it is sufficient to replace u with the variable 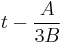 :
:
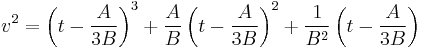 ;
;
finally, this gives the equation:
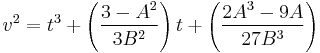 .
.
See also
- Table of costs of operations in elliptic curves, information about the running-time required in a specific case
Notes
References
- Peter L. Montgomery (1987). Speeding the Pollard and Elliptic Curve Methods of Factorization. American Mathematical Society. JSTOR 2007888.
- Daniel J. Bernstein, Peter Birkner, Marc Joye, Tanja Lange and Christiane Peters (2008). Twisted Edwards Curves. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-68159-5. http://www.springerlink.com.proxy.library.uu.nl/content/m37m171510425501/fulltext.pdf.
- Wouter Castryck, Steven Galbraith, Reza Rezaeian Farashahi. Efficient Arithmetic on Elliptic Curves using a Mixed Edwards-Montgomery Representation. http://wis.kuleuven.be/algebra/castryck/xcoordinate.pdf.